かの「 第 9 回 JOI 予選 5 問題 (失敗編) 」以来、 僕は学校へ行っても家へ帰っても、頭を悩ませ続けました。 問題の解説を普通に読んでもワケワカメ、完全にお手上げ状態でした。

そこである日の朝、部活の顧問の先生に問題を見せ、 「どういうことですかね？」と解説を乞いました。 そしてその日の帰り部、なんと先生はExcelのVBAを巧みに使って解いてしまいました。 しかし解法は数式だらけの解法２を使った解き方で、 やっぱり数学ができなければ問題５ともなるとできないのかな、と思い始めました。 それが昨日の帰りの話です。

今朝は、もうテスト週間も近いのでテスト勉強をする気満々で学校へ行きました。 部活についてもあまり JOI のことは考えず、部活の仲間と簿記の勉強をしていました。

教室へ行き、ペラペラと問題 5 の解説の印刷をめくりつつ、 力紙 (ちからがみ、通称りきし。印刷ミスのわら半紙のウラ面を使えるようにホチキスで留めた計算用紙。) になにやら自分でもわからない図形やらなんやらを書いていると、 なんと式で解けてしまったのです。

そして今日の帰り部にて、早速コーディングを行いました。 但し C/C++ コンパイラは Online C Compiler などを使うしかありません。 学校の PC に GCC 入れたいんですけどね；； まあ、Online Compiler はデバッグがとてもしにくいので、 自宅で書き直しました。すると、なんとか動きました。

以下ソースコード。

#include <stdio.h>
#include <string.h>

int main(){
  int w, h, temp, result;
  scanf("%d %d", &w, &h);
  unsigned int tate[w][h-1][2], yoko[w-1][h][2];  //tate、yoko、それぞれ[0]が可曲、[1]が不曲
  memset(tate, 0, sizeof(tate));
  memset(yoko, 0, sizeof(yoko));
  tate[0][0][0] = 1;
  yoko[0][0][0] = 1;
  for(int times = 0; times < w * 2 - 1; times++){
    if(times % 2 == 0){
      /*タテの辺の処理*/
      temp = times / 2;
      for(int i = 0; i < h - 1; i++){
        if(i != 0) tate[temp][i][0] += (tate[temp][i - 1][0] + tate[temp][i - 1][1]) % 100000;  //可曲の計算
        if(temp != 0) tate[temp][i][1] += yoko[temp - 1][i][0] % 100000;    //不曲の計算
      }
    }else{
      /*ヨコの辺の処理*/
      temp = times / 2;
      for(int i = 0; i < h; i++){
        if(temp != 0) yoko[temp][i][0] += (yoko[temp - 1][i][0] + yoko[temp - 1][i][1]) % 100000;   //可曲の計算
        if(i != 0) yoko[temp][i][1] += tate[temp][i - 1][0] % 100000;   //不曲の計算
      }
    }
  }
  result = (tate[w-1][h-2][0] + tate[w-1][h-2][1] + yoko[w-2][h-1][0] + yoko[w-2][h-1][1]) % 100000;
  printf("ANS:%d\n", result);
}

結果、前回の再帰で作ったソースコードよりも短く早くなりました。めでたしめでたし。

解説

あとで読んでみたら、まんま解説１通りでした。しかし、確かに解説が少しわかりにくいのも確かです。少し解説したいと思います。

まず、問題を確認するとJOIさんの住む街は、京都の碁盤の目のような構造になっていることが分かります。

これを見ると「交差点」に目がいきそうになるのですがそこはぐっとこらえて、交差点と交差点を結ぶ「道路」、解説の言葉を借りれば「辺」に着目してください。この「辺」それぞれに、「そこへ、曲がれる状態でたどり着く場合の数」「そこへ、曲がれない状態でたどり着く場合の数」を書いていきます。

例えば入力例１で考えると、この図のようになりますね。

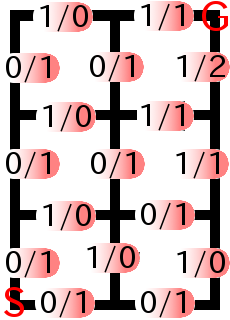
スラッシュの右が曲がれる時の数(可曲と表す)、左が曲がれない時の数(不曲と表す)です。すると、スタート地点などの「可曲な状態」では「0/1」、角の隣などの「不曲な状態」では「1/0」が多いということを頭に入れておいてください。

そして、Gに隣接する「1/1」、[1/2」のそれぞれの数字を足し、1+1+1+2=5で５通り、と計算をします。

さて、可曲と不曲の計算をまとめると、次のようになります。

縦向きの辺の可曲…丁度下にある縦向きの辺の不曲と可曲を足したもの

縦向きの辺の不曲…この辺の下から左に伸びる横向きの辺の可曲

横向きの辺の可曲…丁度左にある横向きの辺の不曲と可曲を足したもの

横向きの辺の不曲…この辺の左端から下に伸びる縦向きの辺の可曲

それぞれの辺が関連しあっているので、計算していく順が重要ですが、それほど難しい話ではありません。JOIさんは右か上にしか進まないわけなので、左下から右上へ計算していけば良い訳です。

この解説を踏まえた上で、もう一度上のソースコードを読んでください。なんとなくわかるでしょうか・・・。

正直、自分にとってはかなり難しい問題でした。ある程度なれておかないとなあ。